

Download Permute 3 for macOS 10.11 or later and enjoy it on your Mac. For an example that counts permutations, see Sample Problem 1. The permutations were formed from 3 letters (A, B, and C), so n = 3 and each permutation consisted of 2 letters, so r = 2. Consider the example from the previous paragraph. Each such matrix, say P, represents a permutation of m elements and, when used to multiply another matrix, say A, results in permuting the rows (when pre-multiplying, to form PA) or columns (when post-multiplying, to form. In mathematics, particularly in matrix theory, a permutation matrix is a square binary matrix that has exactly one entry of 1 in each row and each column and 0s elsewhere. All four numbers must be used and each number may only be used once. Using the numbers 1, 3, 4 and 6, create an algebraic expression that equals 24. Download source - 13.21 KB A Simple Problem. Use the squeeze function to remove the third dimension, resulting in a 3-D array.Datasets, Transforms and Models specific to Computer Vision - pytorch/vision. For example, use the repmat function to create a 2-by-3-by-1-by-4 array whose elements are each 5, and whose third dimension has length 1. The squeeze function performs another type of manipulation that eliminates dimensions of length 1. When working with multidimensional arrays, you might encounter one that has an unnecessary dimension of length 1.

Similarly, interchange row and page subscripts of M. The original rows of M are now columns, and the columns are now rows. Use the permute function to interchange row and column subscripts on each page by specifying the order of dimensions in the second argument. Permutations are used to rearrange the order of the dimensions of an array. Reshape operates columnwise, creating the new matrix by taking consecutive elements down each column of A, starting with the first page then moving to the second page. Use the reshape function to rearrange the elements of the 3-D array into a 6-by-5 matrix. Reshaping a multidimensional array can be useful for performing certain operations or visualizing the data. reshape, permute, and squeeze are useful functions for rearranging elements.
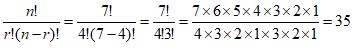


 0 kommentar(er)
0 kommentar(er)
